Die von Paul Kubelka und Franz Munk 1931 entwickelte Theorie beschreibt, unter bestimmten Voraussetzungen, die Lichtabsorption und Lichtstreuung von pigmentierten Systemen (z.B. Farbanstrichen oder Farbstoffen in Textilien). Die sogenannte Kubelka-Munk Theorie kann aus Messungen zweier Schichtdicken voraussagen, welche Farbe bei anderen Schichtdicken entsteht. Damit kann abgeschätzt werden, wie viel Pigmente man beimischen muss, damit die Farbe bei einer bestimmten Dicke des Auftrags deckend ist.
Die Zweikonstanten-Theorie versucht, durch ein stark vereinfachtes Model der Wege der Lichtstrahlen, die wellenlängenabhängige Reflexion R in Abhängigkeit des Absorptionskoeffizienten k(λ) und des Streukoeffizienten s(λ) sowie der Untergrund-Reflexion, Schichtdicke und der Konzentrationen der Pigmente, berechenbar zu machen.
Sie wurde entwickelt, um die Analyse von Materialien wie Papieren und Pulvern zu erleichtern. Das gemeinsame Merkmal dieser Materialien ist die innere In-Homogenität. Die Ausbreitung von Licht in solchen inhomogenen Medien unterscheidet sich erheblich von der Lichtausbreitung in einem homogenen Material.
Annahmen
Diese Theorie wurde ursprünglich für Lackfilme entwickelt, funktioniert aber in vielen Fällen sehr gut für Papier (jedoch nicht ausreichend genau für dunkel gefärbte Papiere, bei denen die Absorption hohe Werte erreicht).
- Eine einschränkende Annahme ist dass die Partikel, aus denen sich die Farbschicht zusammensetzt, viel kleiner sein müssen als deren Gesamtdicke und in der Schicht fixiert sind.
- Im Idealfall sollte die Beleuchtung sollte mit diffusem monochromatischem Licht erfolgen.
- Das Lambert’sche Kosinusgesetz wird als gültig angenommen (isotrope Streuverteilung).
- Die Theorie funktioniert am besten für optisch dicke Materialien, bei denen > 50 % des Lichts reflektiert wird und < 20 % transmittiert wird
Übersicht
Betrachten Sie Licht der Intensität I0, das auf ein nicht glänzendes Papier der Dicke X und des Reflexionsgrades R fällt und sich außerdem seitlich sehr weit („unendlich“) erstreckt.
Unter diesem Stück Papier befindet sich eine Unterlage mit dem Reflexionsgrad R'.
Das Licht, das nach Streuung, Absorption oder Transmission von der Oberseite des Papiers wieder austritt, hat die Intensität I'. In einem Abstand x von der Unterseite des Papiers befindet sich eine dünne Schicht der Dicke dx, auf die gestreutes Licht trifft, das sich sowohl nach oben als auch nach unten mit den Intensitäten i bzw. j bewegt.
Diese dünne Schicht hat, wie jeder andere Bereich des Papiers, den Absorptionskoeffizienten k und den Streukoeffizienten s.
k ist der Absorptionskoeffizient ≡ der begrenzende Anteil der Absorption von Lichtenergie pro Einheitsdicke, da die Dicke sehr klein wird.
k ist der Streukoeffizient ≡ der begrenzende Anteil der rückwärts gestreuten Lichtenergie pro Einheitsdicke, da die Dicke zu Null tendiert.
Der Effekt des Materials mit einer dünnen Schicht dx lässt sich wie folgt beschreiben:
- Abschwächung von i mit i (s + k) dx (Absorption und Streuung)
- Abschwächung j mit j (s + k) dx (Absorption und Streuung)
- Verstärkung von i mit j S dx (gestreutes Licht von j verstärkt i)
- Verstärkung j mit i S dx (gestreutes Licht von i verstärkt j)
Die Änderungen lassen sich in zwei gekoppelten Differenzialgleichungen formulieren lassen; zu beachten ist die gegensätzliche Orientierung (Vorzeichen) von di und dj:
Formel
R∞, die Remission einer „unendlich“ dicken, deckenden Schicht, wird wie folgt bestimmt:

R∞ einer Schicht kann in der Praxis ersetzt werden durch eine Schicht die ausreichend dick ist, sodass das Messgerät zur nächst dickeren Schicht keinen Unterschiede mehr detektiert.
Kubelka-Munk-Funktion
Die Formel lässt sich, bei ausreichenden Kenntnissen, und wenn die Untergrundremission keine Rolle spielt leicht umformen in die bekannte Kubelka-Munk-Funktion:
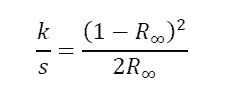
Die rechte Seite kann messtechnisch bestimmt werden. Die Theorie geht davon aus, dass k und s bei unterschiedlichen Farbdicken konstant sind.
Alle Größen gelten spezifisch je Wellenlänge λ allerdings wird es aus Gründen der Übersichtlichkeit in den Formeln weggelassen.
Die K-M-Transformation der gemessenen spektroskopischen Beobachtungen ist annähernd proportional zum Absorptionskoeffizienten und damit annähernd proportional zur Konzentration.
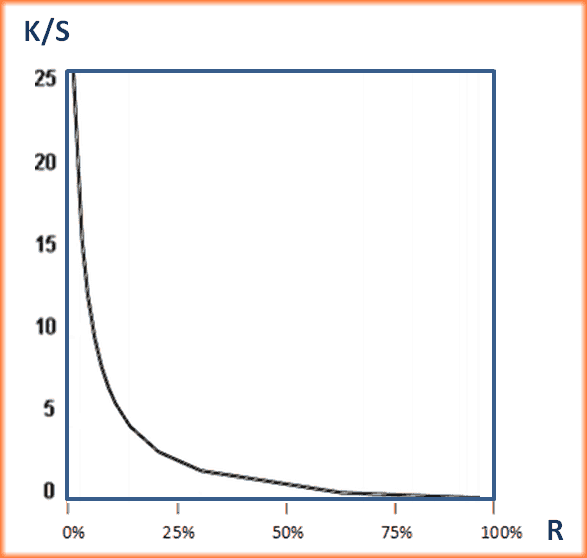
Quotient von K/S und Relation zu R
Durch die Wahl eines geeigneten Aufhellungsmittels kann man versuchen das Minimum der R-Werte auf den Bereich von 10% - 30% zu beschränken.
Streukoeffizient
Der Streukoeffizient s wurde in die theoretische Beschreibung der diffusen Reflexion als semi-empirischer Parameter zur Berücksichtigung der internen Streuprozesse eingeführt.
Er wird durch die Partikelgröße und den Brechungsindex der Probe dominiert. Es besteht eine strake Korrelation zur der Wellenlänge und des Absorptionskoeffizienten, so dass das K-M-Modell es als eine Konstante betrachtet.
In Wirklichkeit variiert der Streukoeffizient langsam mit der Wellenlänge. Noch wichtiger ist, dass er sich mit der Packungsdichte signifikant ändert, daher sollte darauf geachtet werden, dass pulverförmige Proben so reproduzierbar wie möglich verpackt werden, wenn quantitative Ergebnisse erforderlich sind.
Literatur
Originalveröffentlichung:
Paul Kubelka, Franz Munk: Ein Beitrag zur Optik der Farbanstriche. In: Zeitschrift für technische Physik. 12, 1931, S. 593–601.
Detaillierte Beschreibung zur Lösung der Differentialgleichungen:
Industrielle Farbprüfung, Grundlagen und Methoden; Lehrbuch von H.G. Völz, VCH, Weinheim, New York, Basel, Cambridge 1990

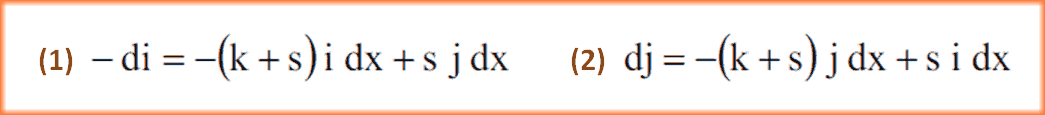
 Impressum
Impressum  Datenschutz
Datenschutz